Question

Solve using fractional law exponent rule

Answer 1

We conclude that:

`\sqrt[5]{8^3}=8^{(3)/(5)}`

Explanation:

Given

We are given the expression

`\sqrt[5]{8^3}`

To determine

Solve using fractional law exponent rule

Given the expression

`\sqrt[5]{8^3}`

Apply radical rule:
`\sqrt[n]{a}=a^{(1)/(n)}`

`\sqrt[5]{8^3}=\left(8^3\right)^{(1)/(5)}`

Apply exponent rule:
`\left(a^b\right)^c=a^(bc)`

`=8^{3\cdot (1)/(5)}`

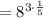
Multiply the exponent: 3 × 1/5 = 3/5

`=8^{(3)/(5)}`

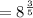
Therefore, we conclude that:

`\sqrt[5]{8^3}=8^{(3)/(5)}`