Question

Anyone can help?? I need this done before 9am please!!

Answer 1

The slopes for each of the four line segments are
`a_(A) = 6\,(m)/(min^(2))`,
`a_(B) = 0\,(m)/(min^(2))`,
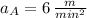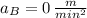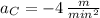`a_(C) = -4\,(m)/(min^(2))` and
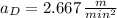`a_(D) = 2.667\,(m)/(min^(2))`, respectively.

Step-by-step explanation:

There are four line segments:

(i) Line A:
`v(0\,min) = 0\,(m)/(min)`,
`v(10\,min) = 60\,(m)/(min)`

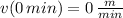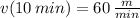
(ii) Line B:
`v(10\,min) = 60\,(m)/(min)`,
`v(15\,min) = 60\,(m)/(min)`

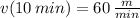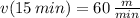
(iii) Line C:
`v(15\,min) = 60\,(m)/(min)`,
`v(40\,min) = -40\,(m)/(min)`

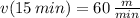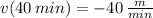
(iv) Line D:
`v(40\,min) = -40\,(m)/(min)`,
`v(55\,min) = 0\,(m)/(min)`

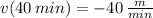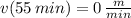
The slope of each line segment represents the acceleration of the particle, which can calculated by the geometrical concept of secant line. Hence, we proceed to determine the acceleration associated with each line segment:

Line A

`a_(A) = (v(10\,min)-v(0\,min))/(10\,min-0\,min)`

`a_(A) = (60\,(m)/(min)-0\,(m)/(min))/(10\,min-0\,min)`

`a_(A) = 6\,(m)/(min^(2))`

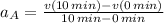
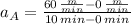
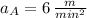
Line B

`a_(B) = (v(15\,min)-v(10\,min))/(15\,min-10\,min)`

`a_(B) = (60\,(m)/(min)-60\,(m)/(min) )/(15\,min-10\,min)`

`a_(B) = 0\,(m)/(min^(2))`

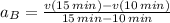
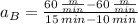
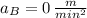
Line C

`a_(C) = (v(40\,min)-v(15\,min))/(40\,min-15\,min)`

`a_(C) = (-40\,(m)/(min)-60\,(m)/(min) )/(40\min-15\,min)`

`a_(C) = -4\,(m)/(min^(2))`

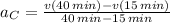
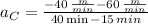
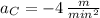
Line D

`a_(D) = (v(55\,min)-v(40\,min))/(55\,min-40\,min)`

`a_(D) = (0\,(m)/(min)-\left(-40\,(m)/(min) \right) )/(55\,min-40\,min)`

`a_(D) = 2.667\,(m)/(min^(2))`

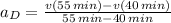
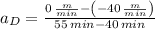
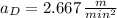
The slopes for each of the four line segments are
`a_(A) = 6\,(m)/(min^(2))`,
`a_(B) = 0\,(m)/(min^(2))`,
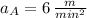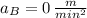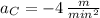`a_(C) = -4\,(m)/(min^(2))` and
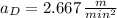`a_(D) = 2.667\,(m)/(min^(2))`, respectively.