Question

HELP!!!!!! I believe its B but I am not sure! :(

Answer 1

A

Explanation:

When solving for x as an exponent, we need to use logarithms in order to undo the operation and rearrange the terms. We use log rules to bring down the exponent and solve. Logarithms are the inverse operations to exponents and vice versa. We have one special kind of logarithm called the natural logarithm whose base is e. We write it as ln. Since our base is e here, we will use the natural logarithm to rearrange and isolate x.

`e^(4x-1) =3`

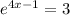
We begin by applying the natural logarithm to each side.

`ln(e^(4x-1)) =ln(3)`

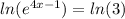
Log rules allow use to rearrange the exponent as multiplication in front of the log.

`(4x-1)ln(e) =ln(3)`

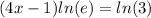
ln e as an inverse simplifies to 1.

`(4x-1)(1)=ln(3)`

We now apply the inverse operations for subtraction and multiplication.

`4x-1+1=1+ln(3)\\4x=1+ln(3)\\(4x)/(4) =(1+ln3)/(4) \\x =(1+ln3)/(4)`

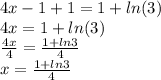
Option A is correct.