a) In order for
 to be continuous at
to be continuous at
 , we need to have
, we need to have
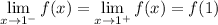
By definition of
 , we know
, we know
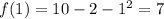 . Meanwhile, the limits are
. Meanwhile, the limits are
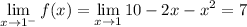
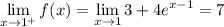
so
 is indeed continuous at
is indeed continuous at
 .
.
b) We use the first derivative test (FDT) here, but when we compute the derivative of a piecewise function, we have to be careful at the points where the pieces "split off", because it's possible that the derivative does not exist at these points, yet an extreme value can still occur there. (Consider, for example,
 at
at
 .)
.)
In this case,
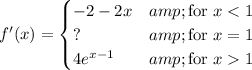
We find the critical points for each piece over their respective domains:
On the first piece:
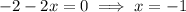
which does fall in [-2, 2]. The FDT shows
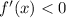 for
for
 less than and near -1, and
less than and near -1, and
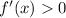 for
for
 greater than and near -1, so
greater than and near -1, so
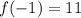 is a local maximum.
is a local maximum.
On the second piece:
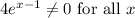
so it does not contribute any critical points.
Where the pieces meet:
By checking the conditions for continuity mentioned in part (a), we can determine that
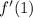 does not exist, but that doesn't rule out
does not exist, but that doesn't rule out
 as a potential critical point.
as a potential critical point.
We have
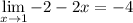
so
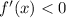 for
for
 less than and near 1, and
less than and near 1, and
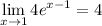
so
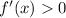 for
for
 greater than and near 1. So the FDT tells us that
greater than and near 1. So the FDT tells us that
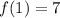 is a local minimum.
is a local minimum.
Finally, at the endpoints of the domain we're concerned with, [-2, 2]:
We have
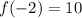 and
and
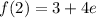 .
.
So, on [-2, 2],
 attains an absolute minimum of
attains an absolute minimum of
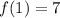 and an absolute maximum of
and an absolute maximum of
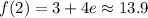 .
.