Question

What is the smallest possible slope for y=x^3 -3x^2 +5x -1

Answer 1

Minimum slope possible for x³ -3x² +5x -1 is 2

Explanation:

We need to find minimum slope for y = x³ -3x² +5x -1

Slope is derivative of y

`\texttt{Slope,}(dy)/(dx)=3x^2-6x+5`

Now we need to find minimum of 3x² -6x +5

At minimum derivative of 3x² -6x +5 is zero

That is

6x - 6 = 0

x = 1

So the slope is minimum at x = 1

At x = 1,

Slope = 3 x 1² -6 x 1 +5 = 2

Minimum slope possible for x³ -3x² +5x -1 is 2

Answer 2

let's find its first derivative for "y"

`\bf y=x^3-3x^2+5x-1\implies \cfrac{dy}{dx}=3x^2-6x+5`

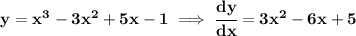
now, we can run the quadratic formula on that derivative, and it turns out we end up with a negative radicand and therefore an imaginary/complex solution, which is a way to say there are no solutions for it, so the quadratic never touches the x-axis.

so hmmm what is the smallest value it goes down to, for the derivative, before it goes right back up?

well, for that we can simply check her vertex location.

`\bf \textit{vertex of a vertical parabola, using coefficients} \\\\ \cfrac{dy}{dx}=\stackrel{\stackrel{a}{\downarrow }}{3}x^2\stackrel{\stackrel{b}{\downarrow }}{-6}x\stackrel{\stackrel{c}{\downarrow }}{+5} \qquad \qquad \left(-\cfrac{ b}{2 a}~~~~ ,~~~~ c-\cfrac{ b^2}{4 a}\right) \\\\\\ \left( -\cfrac{(-6)}{2(3)}~~,~~5-\cfrac{(-6)^2}{4(3)} \right)\implies \left( 1~~,5-\cfrac{36}{12} \right) \\\\\\ (1~,~5-3)\implies (\stackrel{x}{1}~,~\stackrel{y}{2})`

so, "y" or dy/dx goes as low as 2 before going back up, and that happens when x = 1.

Check the picture below.