Question

Which expression represents a circle with a center at (2, -8) and a radius of 11?

Answer 1

(x - 2)² + (y + 8)² = 121

Explanation:

the equation of a circle in standard form is

(x - h)² + (y - k)² = r²

where (h, k) are the coordinates of the centre and r is the radius

here (h, k) = (2, - 8) and r = 11, hence

(x - 2)² + (y + 8)² = 121

Answer 2

The equation
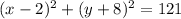`\((x-2)^2 + (y + 8)^2 = 121\)` represents a circle with a center at (2, -8) and a radius of 11. This is derived from the general circle equation
`\((x - h)^2 + (y - k)^2 = r^2\).`

The correct equation representing a circle with a center at (2, -8) and a radius of 11 is option (b)
`\((x-2)^2 + (y + 8)^2 = 121\)`.

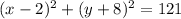The general equation of a circle is
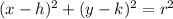`\((x - h)^2 + (y - k)^2 = r^2\)`, where (h, k) is the center and r is the radius.

In option (b),
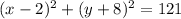`\((x-2)^2 + (y + 8)^2 = 121\)`, the values match the given center (2, -8) and radius of 11. The squared terms with (x-2) and (y+8) are in the correct form, and the radius squared
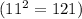`(\(11^2 = 121\))` is on the right side.

Options (a), (c), and (d) do not represent the given circle because they have incorrect signs, centers, or radius values. Therefore, the correct equation is option (b).