1. The direction of the vector
 relative to the positive x-axis satisfies
relative to the positive x-axis satisfies
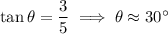
2. A vector with magnitude
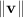 and direction
and direction
 has component form
has component form
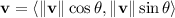
We have
 , but "angle of 60 degrees with the negative x-axis" is a bit ambiguous. I would take it to mean "60 degrees counterclockwise relative to the negative x-axis", so that the direction is
, but "angle of 60 degrees with the negative x-axis" is a bit ambiguous. I would take it to mean "60 degrees counterclockwise relative to the negative x-axis", so that the direction is
 . Then
. Then
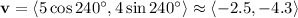
But this doesn't match any of the options, so more likely it means the angle is 60 degrees clockwise relative to the negative x-axis, in which case
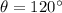 and we'd get
and we'd get
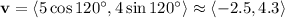
3. Same as question 2, but now we're using
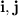 notation. The vector has magnitude
notation. The vector has magnitude
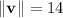 and its direction is
and its direction is
 . So the vector is
. So the vector is
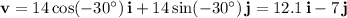
4. The velocity of the plane relative to the air,
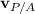 is 175 mph at 40 degrees above the positive x-axis. The velocity of the air relative to the ground,
is 175 mph at 40 degrees above the positive x-axis. The velocity of the air relative to the ground,
 , is 35 mph at 60 degrees above the positive x-axis. We want to know the velocity of the plane relative to the ground,
, is 35 mph at 60 degrees above the positive x-axis. We want to know the velocity of the plane relative to the ground,
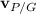 .
.
We use the relationship
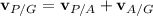
Translating the known vectors into component form, we have
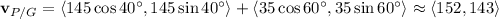
This vector has magnitude and direction

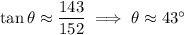
(or 43 degrees NE)