1. If
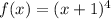 , then
, then
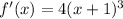 . So
. So
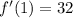 .
.
2. With
 , we differentiate once with respect to
, we differentiate once with respect to
 and get
and get
![(\mathrm d)/(\mathrm dx)[x^2+y^2]=(\mathrm d)/(\mathrm dx)1](https://img.qammunity.org/2019/formulas/mathematics/middle-school/prjep0c75qte8xvwlmibd7bln8rxbcs173.png)
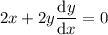
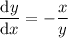
Differentiate again with respect to
 and we get
and we get

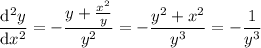
(where
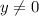 ).
).
3. Check the one-side limits where the pieces are split. For
 to be continuous everywhere, we need
to be continuous everywhere, we need
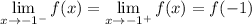
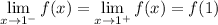
In the first case, we have
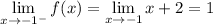
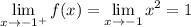
and
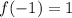 , so it's continuous here.
, so it's continuous here.
In the second case, we have
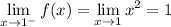
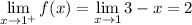
so
 is discontinuous at
is discontinuous at
 .
.
4. If
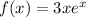 , then
, then
![f'(x)=3e^x+3xe^x=3e^x(1+x)[tex]. So [tex]f'(0)=3](https://img.qammunity.org/2019/formulas/mathematics/middle-school/jeranqve4oaymetojxn2pmrhte2r3o2d7o.png) .
.
5. If
 , then
, then
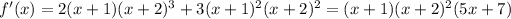 . So
. So
 .
.
6. The average velocity over [1, 2] is given by
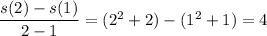
7. If
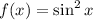 , then
, then
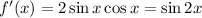 . So
. So
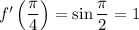 .
.
8. If
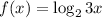 , then
, then
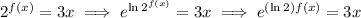
Differentiating, we get
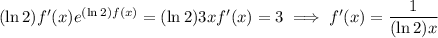
So
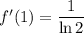 .
.
9. If
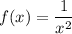 , then
, then
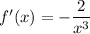 . So
. So
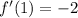
10. If
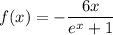 , then
, then
 . So
. So
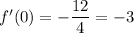 .
.