Answer:
The excluded values of given expression are 5 and 7.
Explanation:
Given expression,
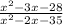
Excluded values are values that will make the denominator of a fraction equal to 0.
Here, the denominator =
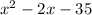
So, for excluded values,
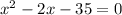
 ( By middle term splitting )
( By middle term splitting )
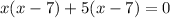
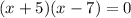
If x + 5 = 0 ⇒ x = -5,
Or If x - 7 = 0 ⇒ x = 7,
Thus, the excluded values of given expression are 5 and 7.