Answer:
The correct answer option is 24 min.
Explanation:
Let us assume t to be Chris's time (in hours) so we can write the following equation:
Samir's time (in hours)
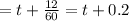
Chris's rate
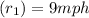
Samir's rate
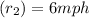
Then putting the values in the formula to get:
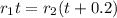
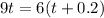
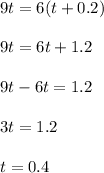
t = 0.4 which will be
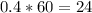
Therefore, Chris catches up Samir after riding for 24 minutes.