Answer: 349.0 gms.
Explanation:
The exponential decay equation is given by :-
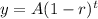 , where A= Initial value , r = rate of decay in decimal and t is time.
, where A= Initial value , r = rate of decay in decimal and t is time.
As per given , we have
A= 640 gm
r= 7.3%=0.073
Then , our decay function will become :-
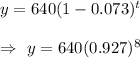
At t= 8 minutes, we have
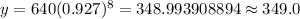
Hence, after 8 minutes , the remaining amount of element = 349.0 gms.