Question

In △ABC, CH=33 ft. What is the length of CX¯¯¯¯¯¯ ? Enter your answer in the box. ft A triangle A B C. Side B C is the base. F, G, and H are the midpoints of sides A F, B G, and C H respectively. Midpoints of each side connect to the opposite vertex. A F is the median of line segment B C. B G is the median of line segment A C. C H is the median of line segment A B. Medians intersect at a point labeled X. Single tick marks are on the line segments A H and H B. Double tick marks are on the line segments B F and F C. Triple tick marks are on the line segments A G and G C.

Answer 1

22 ft

Explanation:

33-1/3(33)=22

Answer 2

The length of CX is 22 ft.

Explanation:

Given information: In triangle ABC, F, G, and H are the midpoints of sides BC, CA, and AB respectively.

The medians FA, BG and CH intersect each other at point X.

According to the property of triangle, the intersection point of medians is called centroid and the centroid divides each median in 2:1.

Since X is centroid, therefore points X divides the median CH in 2:1, therefore we can say that CX:XH is 2:1.

It is given that the length of CX is 33.

`CX=(2)/(3)CH`

`CX=(2)/(3)* 33`

`CX=2* 11`

`CX=22`

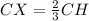
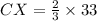
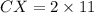
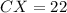
Therefore the length of CX is 22 ft.