Question

Berto invested in a precious mineral. The value of the mineral tends to increase by about 11% per year. He invests $40,000 in 2015.

How much more will his investment be worth in 2020?



Enter your answer in the box.

Round to the nearest whole dollar.

Answer 1

Explanation:

20742

Answer 2

$27402.

Explanation:

We have been given that Berto invested in a precious mineral. The value of the mineral tends to increase by about 11% per year. He invests $40,000 in 2015.

Let us write a function using our given information for the value of minerals.

We are told that the value of minerals increase by 11% every year, so our function will be an exponential function.

Since an exponential function is in form:
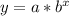`y=a*b^x`; for growth b=(1+r), where r is rate of growth in decimal form.

a= Initial value.

Let us convert our given rate in decimal form.

`11 percent= (11)/(100)=0.11`

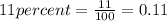
Let G(t) be the growth of minerals t years after 2015.

Upon substituting our given values we will get our function as:
`G(t)=40,000*(1+0.11)^t`

`G(t)=40,000*(1.11)^t`

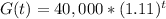
To find the value of Berto's investment in year 2020 by substituting t=5 in our function as 2020-2015=5.

`G(2020)=40,000*(1.11)^5`

`G(2020)=40,000*1.6850581551`

`G(2020)=67402.326204\approx 67402`

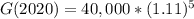
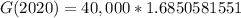
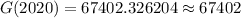
Therefore, the value of his investment in 2020 will be $67402.

Let us find the difference of values of minerals between 2020 and 2015.

67402-40000=27402

Therefore, Berto's investment will be worth $27402 in 2020.