Question

In an effort to control vegetation overgrowth, 139 139 rabbits are released in an isolated area free of predators. After 2 2 years, it is estimated that the rabbit population has increased to 556 556 . Assuming exponential population growth, what will the population be after another 6 6 months? Round to the nearest rabbit.

Answer 1

197

Explanation:

Initial population of rabbit is 139

after 2 years , rabbit population is 556

For exponential growth use y=ab^x

where a is the initial population

x is the time period

b is the growth rate, y is the final population

a= 139 is already given

when x=2, the value of y = 557

plug in all the values in the formula and find out 'b'

`y=ab^x`

`557=139(b)^2`

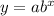
Divide both sides by 139

`(557)/(139) =b^2`

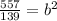
take square root on both sides

b=2.00180 and b=-2.00180

growth factor cannot be negative

So b= 2.0018

The equation y=ab^x becomes

`y=139(2.0018)^x`

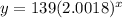
To find population after 6 months

1 year = 12 months

so 6 months = 0.5 years

we plug in 0.5 for x

`y=139(2.0018)^(0.5)`

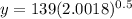
y= 196.66

so population after 6 months = 197