Answer:
22.5
Explanation:
If you expand the series, you can see the first few terms of the series:
- Putting 1 in
 ,
,
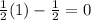
- Putting 2 in
 ,
,

- Putting 3 in
 ,
,
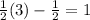
- Putting 4 in
 ,
,
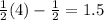
We can see the series is 0, 0.5, 1, 1.5, ....
This is an arithmetic series with common difference (the difference in 2 terms) 0.5 and first term 0.
We know formula for sum of arithmetic series:
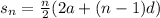
Where,
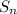 denotes the nth partial sum
denotes the nth partial sum
 is the first term (in our case it is 0)
is the first term (in our case it is 0)
 is the term (in our case it is 10 since we want to find 10th partial sum -- sum until first 10 terms)
is the term (in our case it is 10 since we want to find 10th partial sum -- sum until first 10 terms)
 is the common difference (difference in term and the previous term) (in our case it is 0.5)
is the common difference (difference in term and the previous term) (in our case it is 0.5)
Substituting these into the formula, we get the 10th partial sum to be:
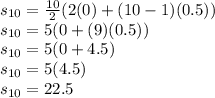
So the sum of the first 10 terms is 22.5. Third answer choice is right.