Question

In parallelogram ABCD , diagonals AC and BD intersect at point E, BE=x^2−40 , and DE=6x .What is BD ? The answer was 120

Answer 1

Answer:hi nice to meet you the answer is 120

Step-by-step explanation:i just took the quiz right now and dont really feel like posting my work right now but for sure 120

Answer 2

120

Explanation:

Given that ABCD is a parallelogram.

We know that in a parallelogram diagonals bisect each other.

Since AC and BD intersect at E, we get E is the mid point of both AC and BD.

Or BE = ED

Substitute the given values for BE and ED

`x^2-40 = 6x\\x^2-6x-40=0\\(x-10((x+4) = =0`

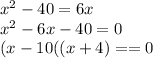
i.e. x =10 or x =-4

But x cannot be negative . So x can take only value 10

BE = DE =6x = 6(10) = 60

Diagonal BD = BE+DE = 60+60 = 120

Answer is 120