Answer:
The system has two distinct solutions.
Explanation:
The given system of equations are:
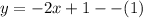
and
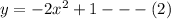
In order to determine the number of solutions the two equations have, we need to equate the two equations to obtain,
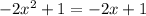
We now group all terms on the left hand side and equate everything to zero.
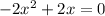
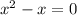
This is now a quadratic equation in
 with
with
 .
.
At this stage we check the number of solutions using the discriminant.
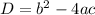

Since the discriminant is greater than zero, the equation will have two distinct roots.
Therefore the system of equations has exactly two distinct solutions.
If you wish to see these solutions, you can continue as follows;
We factor
 to obtain,
to obtain,
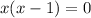

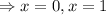
When
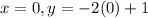
Then we have,

When
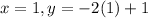
Then we have,
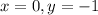
See graph