Question

Question Part Points Submissions Used Determine whether or not F is a conservative vector field. If it is, find a function f such that F = â‡f. (If the vector field is not conservative, enter DNE.) F(x, y) = (y2 â’ 4x)i + 2xyj f(x, y) =

Answer 1

Looks like we have

`\hat F(x,y)=(y^2-4x)\,\hat\imath+2xy\,\hat\jmath`

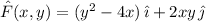
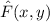`\hat F(x,y)` is conservative if we can find a scalar function
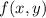`f(x,y)` such that
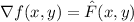`\\abla f(x,y)=\hat F(x,y)`. For this to be the case, we would need to have

`(\partial f)/(\partial x)=y^2-4x`

`(\partial f)/(\partial y)=2xy`

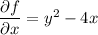
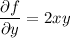
Take the first partial differential equation. If we integrate both sides with respect to
`x`, we'd get

`\displaystyle\int(\partial f)/(\partial x)\,\mathrm dx=\int(y^2-4x)\,\mathrm dx`

`\implies f(x,y)=xy^2-2x^2+g(y)`

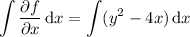
Differentiating both sides with respect to
`y`, we recover the other partial derivative and find

`(\partial f)/(\partial y)=2xy+(\mathrm dg)/(\mathrm dy)=2xy\implies(\mathrm dg)/(\mathrm dy)=0\implies g(y)=C`

where
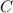`C` is an arbitrary constant. So we've found

`f(x,y)=xy^2-2x^2+C`

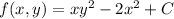
which means that
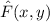`\hat F(x,y)` is conservative.