Question

What is the sum of the infinite geometric series represented by (picture)

A. 240

B. 360

C. 135

D. 720


(please help)

Answer 1

ANSWER

D.

`720`


Step-by-step explanation

The infinite geometric series given to us is,


`\sum_(n=1)^(\infty)180* ((3)/(4))^(n-1)`


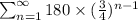
The first term of this series is,




`a_1=180* ((3)/(4))^(1-1)`

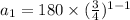
This implies that,


`a_1=180* ((3)/(4))^(0)`



`a_1=180`



`a_2=180* ((3)/(4))^(2-1)`



`a_2=180* ((3)/(4))^(1)`




`a_2=135`



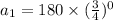
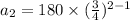
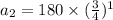
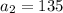
The common ratio of this sequence,




`r = (a_2)/(a_1)`



`r = (135)/(180)`



`r = (3)/(4)`


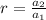
The sum to infinity of this series is given by the formula,


`S_(\infty)=(a_1)/(1 - r)`


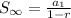
We substitute the above values to get,


`S_(\infty)=(180)/(1 - (3)/(4) )`


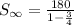
This simplifies to


`S_(\infty)=(180)/( (1)/(4) )`

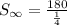
This implies that,


`S_(\infty)=180 * 4`



`S_(\infty)=720`

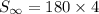
The correct answer is D.