Question

Adam had 30 less balloons than Billy had. After Billy gave 5 balloons to Adam, the number of Adam's balloons was half of the number of Billy's balloons. What was the number of balloons they have together?

Answer 1

60 balloons.

Step-by-step explanation:

Let the number of balloons that Adam had be x and number of balloons Billy had be y.

We have been given that Adam had 30 less balloons than Billy. We can represent this information in an equation as:
`x+30=y...(1)`.

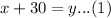If Billy gave 5 balloons to Adam, Billy will have y-5 balloons and Adam will have x+5 balloons.

We are told that x+5 is half of the y-5. Let us represent this information in an equation.

`2(x+5)=y-5...(2)`

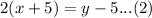
Now we have two equations and to unknowns. Let us solve our system of equations using substitution method.

Upon substituting y's value from equation 1 into equation 2 we will get,

`2(x+5)=x+30-5`

`2(x+5)=x+25`

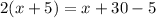
Upon distributing 2 on left side of our equation we will get,

`2x+10=x+25`

`2x-x+10=25`

`2x-x=25-10`

`x=15`

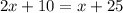
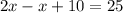
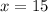
Therefore, Adam has 15 balloons.

Now let us substitute x=15 in equation 1 to find y.

`15+30=y`

`45=y`

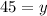
Therefore, Billy has 45 balloons.

Now we will add 45 and 15 to find the number of balloons that Adam and Billy have together.

`\text{Number of balloons Adam and Billy have together}=15+45`

`\text{Number of balloons Adam and Billy have together}=60`

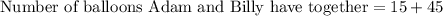
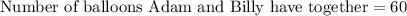
Therefore, Adam and Billy have 60 balloons together.