Question

Given: ∆ABC, AB = BC, BM = MC
AC = 40, m∠BAC = 42º
Find: AM

Answer 1

31.32208078, for those that need the more accurate answer. The steps are pretty much the same as the first answer. Just thought this would be helpful.

Answer 2

The length of AM is 26.50 units.

Explanation:

Given information: AB = BC, BM = MC , AC = 40, ∠BAC = 42º.

Since two sides of triangle are equal, therefore the triangle ABC is an isosceles triangle.

The corresponding angles of congruents sides are always equal. So angle C is 42º.

According to the angle sum property the sum of interior angles is 180º.

`\angle B=180-42-42=96`

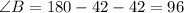
Law of Sine

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

`(\sinB)/(AC)=(\sin(C)/(AB)`

`(\sin(96))/(40)=(\sin(42)/(AB)`

`AB\sin(96)=40\sin(42)`

`AB=(40\sin(42))/(\sin(96))`

`AB=26.91`

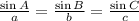
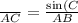
Therefore the length of AB and BC is 26.91.

Since M is midpoint of BC, so

`BM=(BC)/(2)=(26.91)/(2)=13.455`

Use Law of Cosine in triangle ABM to find the value of AM.

`a^2=b^2+c^2-2bc\cos A`

`AM^2=AB^2+BM^2-2(AB)(BM)\cos (B)`

`AM^2=(26.91)^2+(13.455)^2-2(26.91)(13.455)\cos (96)`

`AM=26.50`

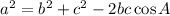
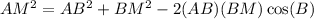
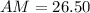
Therefore the length of AM is 26.50 units.