Question

What is the equation of the quadratic graph with a focus of (6, 0) and a directrix of y = −10?

f(x) = −one twentieth (x − 6)2 + 5

f(x) = −one twentieth (x − 6)2 − 5

f(x) = one twentieth (x − 6)2 + 5

f(x) = one twentieth (x − 6)2 − 5

Answer 1

Last option is right

f(x) = one twentieth (x − 6)2 − 5

Explanation:

Given that it is a quadratic equation

Hence a parabola

Focus = (6,0)

Directrix is y =-10

Since vertex lies exactly in the middle from focus to directrix we have

vertex = (6,-5)

The parabola is having axis perpendicular to directrix and hence axis is x =6

The parabola is open up since focus lies above the directrix.

So equation is

`f(x) = ((x-6)^2)/(2) -5`

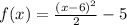
Hence last option is right

f(x) = one twentieth (x − 6)2 − 5