Question

a(t)=(t−k)(t−3)(t−6)(t+3) is a polynomial function of tt, where kk is a constant. Given that a(2)=0a(2)=0, what is the absolute value of the product of the zeros of aa? Answer:

Answer 1

The absolute value of the product of the zeros of a(t) is 108.

Step by step explanation:

The given polynomial function is

`a(t)=(t-k)(t-3)(t-6)(t+3)`

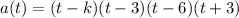
Where k is the constant.

To find the zeros of a(t), equate the polynomial equal to zero.

`(t-k)(t-3)(t-6)(t+3)=0`

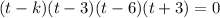
By using zero product property, equate each factor equal to zero.

`t-k=0`

`t=k`

`t-3=0`

`t=3`

`t-6=0`

`t=6`

`t+3=0`

`t=-3`

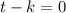
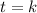
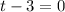
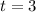
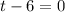
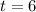
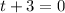
Therefore the zeros of the function are k, 3, 6 and -3. Since it is given that

`a(2)=0`

Therefore, 2 is a zero of a(t). So, the value of k is 2.

The product of zeros is

`2* 3* 6* -3=-108`

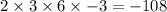
The absolute value of the product is 108.