Answer:
Yes , triangle DEF is congruent to JKL
Explanation:
Given:
The coordinates of triangle DEF are;
D (2, 0)
E(5. 0)
F(5, 5)
and
the coordinates of triangle JKL are:
J(3, -7)
K(6, -7)
L (6, -2)
The rule of translation is used on triangle DEF to get triangle JKL:
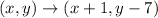
i.e
 = J
= J
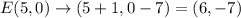 = K
= K
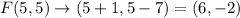 = L
= L
As, we know that two triangles are known as congruent if there is an isometry mapping one of the triangles to the other.
therefore, triangle DEF congruent to triangle JKL