Question

A sample from a fossil has 2 grams of carbon 14. This same sample had 10 grams of carbon 14 at the moment of its demise. If the half-life of carbon 14 is 5730 years, then what is the age of the fossil?

options:

12705 years


13005 years


13105 years


13205 years


13305 years

Answer 1

The correct option is: 13305 years

Explanation:

Formula for radioactive decay is:
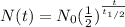`N(t)= N_(0)((1)/(2))^(t)/(t_(1/2))` , where
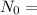`N_(0)=` Initial amount,
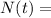`N(t)=` Final amount after
`t` years and
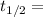`t_(1/2)=` Half-life in years.

Given that, the sample from a fossil has 2 grams of carbon 14 and it had 10 grams of carbon 14 at the moment of its demise.

That means,
`N_(0)= 10 grams, N(t)= 2 grams`

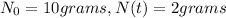
The half-life of carbon 14 is 5730 years. So,
`t_(1/2)= 5730` years.

Now according to the above formula, we will get......

`2= 10((1)/(2))^(t)/(5730) \\ \\ (2)/(10)=((1)/(2))^(t)/(5730) \\ \\ (1)/(5)=((1)/(2))^(t)/(5730)`

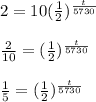
Taking logarithm on both sides......

`log((1)/(5))=log((1)/(2))^(t)/(5730)\\ \\ log((1)/(5))=(t)/(5730)log((1)/(2))\\ \\ (t)/(5730)=(log((1)/(5)))/(log((1)/(2)))\\ \\ t=5730*(log((1)/(5)))/(log((1)/(2)))= 13304.647... \approx 13305`

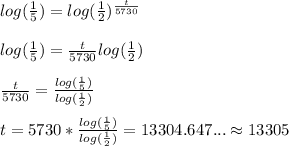
Thus, the age of the fossil is 13305 years.