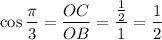Question

How cos π/3=1/2?
having some problems learning continuity.

Answer 1

You can show that
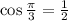`\cos\frac\pi3=\frac12` by constructing a triangle.

Take two points, O(0, 0) and A(1, 0), and let B be the point on the unit circle such that the angle between the line segments OA and OB is
`\frac\pi3` radians.

Since both A and B lie on the circle, the line segments OA and OB both have length 1 (same as the circle's radius). We finish constructing the triangle by connect A and B.

Since OB and OA have the same length, triangle OAB is isosceles, but more than that, it's also equilateral. Why? Because the interior angles of any triangle always add to
`\pi` radians. We know one of the angles is
`\frac\pi3` radians, which leaves a contribution of
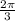`\frac{2\pi}3` radians between the remaining angles A and B. Angles A and B must be congruent (because OAB is isosceles), which means they also have measure
`\frac\pi3` radians.

Next, draw an altitude of the triangle through point B, and label the point where it meets the "base" OA, C. Since OAB is equilateral, the altitude BC is also a perpendicular bisector. That means OC has length
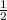`\frac12`, and by definition of
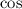`\cos` we have

`\cos\frac\pi3=(OC)/(OB)=\frac{\frac12}1=\frac12`