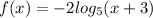The correct answer is:

(In compact form:
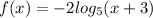 )
)
Step-by-step explanation:
Follow these steps...
1. As it is a logarithmic graph, but reflected along x-axis, the general form of the function will be the following:
f(x) = -a*log(x) + k --- (A)
Where a represent the scale of the logarithmic graph, and k represents whether the graph is shifted down or up.
The negative sign indicates that the graph is reflected along the x-axis.
2. The vertical asymptote is at x = -3, the equation (A) will now become the following:
f(x) = -a*log(x + 3) + k --- (B)
The (x+3) part of the above equation shows that the graph is shifted 3 units towards left.
3. Now we need to find k and a. For finding k, plug in the point (-2,0) in equation (B):
0 = -a*log(-2+3) + k
0 = -a*0 + k
k = 0
4. For finding a, plug in the point (2,-2) and the value of k=0 in equation (B):
-2 = -a*log(2+3) + 0
a = 2/log(5)
Now plug in the values of a and k in equation (B), you will get the answer:
f(x) = -(2/log(5))*log(x+3) + 0
Therefore, the correct answer is:

or, in compact form: