Question

Suppose the average height of all humans is normally distributed with a mean of 72 inches and a variance of 18 inches.

a. Determine P(7580)
b. Determine P(x<65)

Answer 1

a) P(75 < x < 80 ) = 0.2088

b) The probability that average height of all humans less than 65

P( X < 65 ) = 0.0495

Explanation:

Step(i):-

Given mean of the Population = 72

Given variance of the Population = 18 inches.

Standard deviation of the Population = √18 = 4.242

Let 'x' be the random variable in Normal distribution

a)

Given X₁ = 75

`Z_(1) = (x_(1) -mean)/(S.D) = (75-72)/(4.242) = 0.70721`

Given X₂= 80

`Z_(2) = (x_(2) -mean)/(S.D) = (80-72)/(4.242) = 1.885`

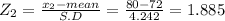
The probability that average height of all humans between 75 and 80

`P(75 < X < 80 ) = P(0.70721 < Z < 1.885)`

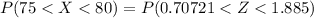
= | A ( 1.885) - A( 0.70721|

= 0.4699 - 0.2611

= 0.2088

P(75 < x < 80 ) = 0.2088

b)

Step(ii):-

Given X₁ = 65

`Z_(1) = (x_(1) -mean)/(S.D) = (65-72)/(4.242) = -1.650`

The probability that average height of all humans less than 65

P( X < 65 ) = P( Z < - 1.650 )

= 1 - P( Z > 1.650)

= 1 - ( 0.5 + A (1.650))

= 0.5 - A( 1.65)

= 0.5 - 0.4505

= 0.0495

The probability that average height of all humans less than 65

P( X < 65 ) = 0.0495