Question

use guess and check to find when an exponential function with a decay rate of 15% per hour reaches half of its original amount, rounded up to the nearest hour. The exponential function reaches half of itsoriginal amount after how many hours?

Answer 1

1.386 or 1 hour

Explanation:

Given that decay rate is 15% per hour.

i.e. y' =-0.15y

Separate the variables and integrate

ln y =-0.15 t +C where t = no of hours

Or
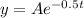`y =Ae^(-0.5t)` where A = initial amount present

When it becomes 1/2 A we have

`A/2 =Ae^(-0.5t)`

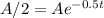
Or
`1/2 =e^(-0.5t)`

`ln(1/2) ={-0.5t}`

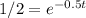
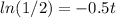
=1.386

In other words in 1 hour (after rounding off) the exponential function reaches its half.