Question

Based on previous studies, researchers believe that 6% of children are born with a gene that is linked to a certain childhood disease. If the researchers test 950 newborns for the presence of this gene, would it be unlikely for them to find fewer than 25 children with the gene? Answer by calculating the appropriate z-score. Round to the nearest hundredth when necessary.

Answer 1

It would be unlikely for them to find fewer than 25 children with the gene.

Explanation:

For large numbers the binomial can be approximated closely by a normal distribution.

So mean and standard deviation of the sample according to binomial distribution will be,

`\mu=n\cdot p=950* 0.06=57`

`\sigma=√(n\cdot p\cdot (1-p))=√(950* 0.06* (1-0.6))=√(950* 0.06* 0.94)=7.32`

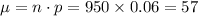
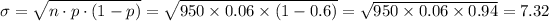
In normal distribution, we know that

`Z=(X-\mu)/(\sigma)=(25-57)/(7.32)=-4.37`

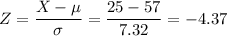
So the confidence interval would be,

`=\overline X\pm Z(s)/(√(n))`

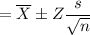
Putting the values,

`=57\pm(-4.37)(7.32)/(√(950))\\\\=55.96,58.03`

As 25 is not in this confidence interval, so it would be unlikely for them to find fewer than 25 children with the gene.