Question

Point G is the centroid of the right △ABC with hypotenuse AB=18 in. Find CG.

Answer 1

CG = 6 in.

Step-by-step explanation:

Given information : Point G is the centroid of the right △ABC with hypotenuse AB=18 in.

We know that circumcenter of a right angle triangle is the midpoint of the hypotenuse.

Let point M be the circumcenter of △ABC.

Hypotenuse AB=18 in.

Radius of circumcircle =
`(18)/(2)=9` in.

Know connect the circumcenter M with the vertex C. CM is a median of the △ABC from vertex C.

MC = radius of the circumcircle = 9 in.

We know that centroid divides each median in a ratio of 2:1.

Point G is the centroid of the right △ABC. It means point G divides CM median in a ratio of 2:1.

`CG=9* (2)/(3)=6`

`GM=9* (1)/(3)=3`

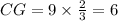
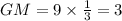
Therefore, the measure of CG is 6 in.

Answer 2

6 in

Step-by-step explanation:

CG is 2/3 the length of median CM, where M is the midpoint of AB. M is the center of the circumscribing circle, which has radius 9 in, so CM is 9 in, and CG is 6 in.