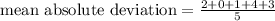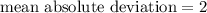Data set: 47, 45, 44, 41, 48 1. Find the mean. Mean = 47 + 45 + 44 + 41 + 48 5 = 225 5 = 45 2. Find each absolute deviation. Absolute deviations: 2, 0, 1, 4, 3 What is the mean …

Question

asked Oct 22, 2019 46.0k views

2 Answers

Martin Theiss · Answer 1 · 2019-10-26T15:22:56+0000

Answer:

We have been given the data: 47,45,44,41,48

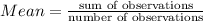
$Mean=\frac{\text{sum of observations}}{\text{number of observations}}$

On substituting the values in the above formula to find mean:

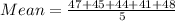
Mean=(47+45+44+41+48)/(5)

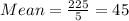
Mean=(225)/(5)=45

Now, we need to find the absolute deviation that is:

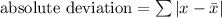
$\text{absolute deviation}=\sum{|x-\bar{x}|}$

Where
$\bar{x}$ is the mean and x is the values given of x which are: 2,0,1,4

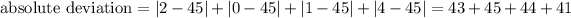
$\text{absolute deviation}=|2-45|+|0-45|+|1-45|+|4-45|=43+45+44+41$

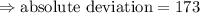
$\Rightarrow \text{absolute deviation}=173$

Now, to find mean absolute deviation we have a formula:

$\text{mean absolute deviation}=\sum\frac{(x-\bar{x})}{N}$

$\text{mean absolute deviation}=(|47-45|+|45-45|+|44-45|+|41-45|+|48-45|)/(5)$

$\text{mean absolute deviation}=(2+0+1+4+3)/(5)$

$\text{mean absolute deviation}=2$