Answer:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \bigg[ 3x^2cosx^3 + 3sin^2(x)cos(x) + 5 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/nvrxg16t6voben55cinkncq6wf8h2415yn.png)
General Formulas and Concepts:
Algebra I
- Functions
- Function Notation
Pre-Calculus
Calculus
Derivatives
Derivative Notation
Derivative Property [Addition/Subtraction]:
![\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/zd1isc8p8d61dms4m7tlsdvpezlc3t2ts1.png)
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/2019/formulas/mathematics/high-school/ijuuby0owovgvvmkyt63pxr8cpkn8j9mgp.png)
Trig Derivative:
![\displaystyle (d)/(dx)[sin(u)] = u'cos(u)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/n1dhjvi060pn5uww32011r6j636bpoxhkd.png)
Explanation:
Step 1: Define
Identify
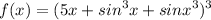
Step 2: Differentiate
- Chain Rule:
![\displaystyle f'(x) = (d)/(dx) \bigg[ (5x + sin^3x + sinx^3)^3 \bigg] \cdot (d)/(dx) \bigg[ 5x + sin^3x + sinx^3 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/8jfvrmd5yy6j37jtvb74doj269z0dmv0re.png)
- Basic Power Rule:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^(3 - 1) \cdot (d)/(dx) \bigg[ 5x + sin^3x + sinx^3 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/6lrj2mnyz4l53vn6210u613wgke3mdfjd5.png)
- Simplify:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot (d)/(dx) \bigg[ 5x + sin^3x + sinx^3 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/kpf8mhjrsqnza5jktpj0jl1kbepuxvd1to.png)
- Derivative Property [Addition]:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ (d)/(dx)[5x] + (d)/(dx)[sin^3x] + (d)/(dx)[sinx^3] \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/tx1mvbd3fdqaso9s4zm0538i5uy4hwte8p.png)
- Rewrite [Trigonometric Notation]:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ (d)/(dx)[5x] + (d)/(dx)[(sinx)^3] + (d)/(dx)[sinx^3] \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/dnd7a7mnvgoch4scy4mld7vx3nsnlf1fs6.png)
- Basic Power Rule:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5x^(1 - 1) + (d)/(dx)[(sinx)^3] + (d)/(dx)[sinx^3] \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/seo6lsj81q666dhjn80041wq89vtbsqz9n.png)
- Simplify:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5 + (d)/(dx)[(sinx)^3] + (d)/(dx)[sinx^3] \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/w4r8kvd4k10zpapqlmyfxbhr54te582bi6.png)
- Trig Derivative [Derivative Rule - Chain Rule]:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5 + (d)/(dx)[(sinx)^3] + \bigg( (d)/(dx)[sinx^3] \cdot (d)/(dx)[x^3] \bigg) \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/jmnl5vt9tzjdlja7qxn68igbore9xb9fk0.png)
- Trig Derivative [Basic Power Rule]:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5 + (d)/(dx)[(sinx)^3] + \bigg( cosx^3 \cdot 3x^(3 - 1) \bigg) \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/h8jomw44d2fpfsrlhqqtq4q0eozb25emsc.png)
- Simplify:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5 + (d)/(dx)[(sinx)^3] + 3x^2cosx^3 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/o8elyv1sovcciysbdahjd8fgjj3cso5gga.png)
- Chain Rule:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5 + \bigg( (d)/(dx)[(sinx)^3] \cdot (d)/(dx)[sinx] \bigg) + 3x^2cosx^3 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/bgrtrd6eitfuwz5iy9ks9pcwpbjs1olx93.png)
- Basic Power Rule:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5 + \bigg( 3(sinx)^(3 - 1) \cdot (d)/(dx)[sinx] \bigg) + 3x^2cosx^3 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/kacxy0o55l6jwe4cs22vexi8in2xl0omyk.png)
- Simplify:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5 + \bigg( 3(sinx)^2 \cdot (d)/(dx)[sinx] \bigg) + 3x^2cosx^3 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/xoi2q80vphetki9xin4s00ndmywlxp2t80.png)
- Trig Derivative:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5 + \bigg( 3(sinx)^2 \cdot cos(x) \bigg) + 3x^2cosx^3 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/mzs3kqt87xrvkar14cwp1i87obykk29hf1.png)
- Simplify [Rewrite]:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \cdot \bigg[ 5 + 3sin^2(x)cos(x) + 3x^2cosx^3 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/8ovmmsmxo62wc7eznrmw5vzzdtu8khami2.png)
- Rewrite:
![\displaystyle f'(x) = 3(5x + sin^3x + sinx^3)^2 \bigg[ 3x^2cosx^3 + 3sin^2(x)cos(x) + 5 \bigg]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/nvrxg16t6voben55cinkncq6wf8h2415yn.png)
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Derivatives
Book: College Calculus 10e