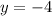The equation of the parabola is given is the Vertex Form. The general form of a quadratic equation in Vertex Form is:
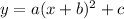
So for our equation,
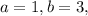 and
and
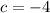 . Now let's solve the question.
. Now let's solve the question.
1. Line of Symmetry:
Line of symmetry is given as
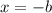 , so our line of symmetry is
, so our line of symmetry is
 .
.
2. Vertex:
Vertex is given as
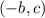 , so our vertex is
, so our vertex is
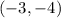 .
.
3. Roots:
We find the roots by setting
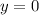 . Thus, we have
. Thus, we have
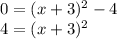
So,
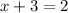 and
and
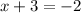
So, solving these 2 equations we have
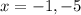
4. Y-Intercept:
To find y-intercept, we set
 . So we have
. So we have
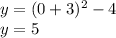
5. Minimum/Maximum:
A quadratic equation has minimum if
 is positive and maximum is
is positive and maximum is
 is negative. Hence, this function has a minimum since
is negative. Hence, this function has a minimum since
 is positive. The value of the minimum is
is positive. The value of the minimum is
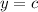 . So for our question, the minimum is
. So for our question, the minimum is
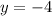 .
.
ANSWERS:
1. Line of Symmetry:

2. Vertex:
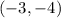
3. Roots:
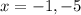
4. y-intercept:
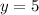
5. Minimum Value: