Question

Which of the following trigonometric expressions is equivalent to csc(-112°)? csc(68°)

cot(112°)
-csc(68°)
csc(112°)

Answer 1

Explanation:

To find:
`\csc \left ( -112^(\circ) \right )`

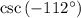
Solution:

Trigonometric expression is an expression consisting of trigonometric ratios like
`\sin ,\tan ,\cos ,\csc ,\cot ,\sec`

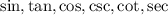
Trigonometric ratios refers to the relation between the sides of right angled triangle and it's angles.

We know that angle
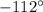`-112^(\circ)` lies in the fourth quadrant in which
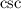`\csc` is negative

So,
`\csc \left ( -112^(\circ) \right )=-\csc \left ( 112^(\circ) \right )`

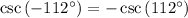
We can write
`-\csc \left ( 112^(\circ) \right )=-\csc \left ( 180^(\circ)-68^(\circ) \right )`

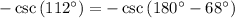
We know that angle
`180^(\circ)-68^(\circ)=112^(\circ)` lies in second quadrant in which
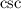`\csc` is positive

`-\csc \left ( 180^(\circ)-68^(\circ) \right )=-\csc68^(\circ)`

Therefore, we get

`\csc(-112^(\circ))=-\csc(112^(\circ))=-\csc \left ( 180^(\circ)-68^(\circ) \right )=-\csc68^(\circ)`

Answer 2

csc(-112°)=-csc(68°)

Explanation:

Since cosec(x) and sin(x) are reciprocals of each other,

cosec(-112°)=
`(1)/(sin(-112^(\circ)))`

=
`(1)/(-sin(112^(\circ)))`

=
`(1)/(-sin(180^(\circ)-68^(\circ)))` (since 112=180-68)

=
`(1)/(-sin(68^(\circ)))` (since sin(180-x)=sinx)

=
`(-1)/(sin(68^(\circ)))` (since
`(a)/(-b)= (-a)/(b)`)

=-cosec(68°)