Question

Posted this question 1000times. Plz some answer plz plz i beg. Plz show all working, thank you sir

Answer 1

`\approx 26.16\:\mathrm{m}`

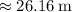
Explanation:

Let
`h` be the height of the tree. In reference to the tree and bird, a right triangle is formed. We can write the following trig function for that right triangle:

`\tan28^(\circ)=(h)/(15),\\h=15\tan28^(\circ),\\h\approx 7.98\:\mathrm{m}`.

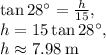Now we can use this to find the hypotenuse of this triangle (the distance between the cat and the bird):

Let the distance between the cat and bird be
`k`. Then,

`7.98^2+15^2=k^2,\\k\approx 16.99\:\mathrm{m}`. This is one side of the triangle that is formed by the cat, bird, and mouse.

The right triangle formed by the tree, cat, and mouse shares the height
`h` with the other right triangle, as we found earlier. Let
`l` represent the hypotenuse of this triangle or the distance between the cat and mouse. We then have the following trig function:

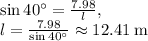`\sin 40^(\circ)=(7.98)/(l),\\l=(7.98)/(\sin40^(\circ))\approx 12.41\:\mathrm{m}`. This is another side of the triangle that is formed by the cat, bird, and mouse.

The triangle that is formed by the cat, bird, and mouse has shares an angle of
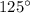`125^(\circ)` with the base of the auxiliary pyramid. The other angles, however, are not shared.

Since we have two sides and the angle between these two sides, we can use the Law of Cosines to find the other side (the distance between the mouse and bird). The Law of Cosines is given by:

`m^2=k^2+l^2-2kl\cos M`, where
`m` is the distance between the bird and the mouse and the other variables are defined above.

Plugging in values, we get:

`m^2=16.99^2+12.41^2-2\cdot16.99\cdot12.41\cdot\cos 125^(\circ)`

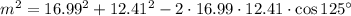
Solving, we get:

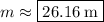`m\approx \fbox{$26.16\:\mathrm{m}$}`.