Answer:
Given:

Prove:
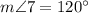
1.
 , by Given.
, by Given.
2.
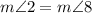 , by Alternate Exterior Angles Theorem.
, by Alternate Exterior Angles Theorem.
3.
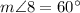 , by substitution.
, by substitution.
4.
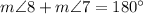 , by Straight Angle Definition and Supplementary Angle Theorem.
, by Straight Angle Definition and Supplementary Angle Theorem.
5.
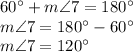 , by substitution.
, by substitution.

It's important to remember that Alternate Exterior Angles are those which are placed outside the parallels and at different sides of the transversal, and these angles are always congruent.
Additionally, the definition of a straight angle is that this angle is equal to 180°, and supplementary angles theorem states that adjacent angles that sum 180° are supplementary one each other.