Answer:
Perimeter of
 is
is
 .
.
Step-by-step explanation:
Given: In
 ,
,
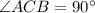 ,
,
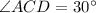 and AD= 8cm.
and AD= 8cm.
In
Sum of the measure of the angles of triangles is 180 degree.
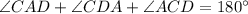
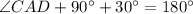 or
or

Simplify:
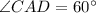
∵ AD= 8cm and
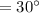 to calculate the length of CD we use tangent ratio i.e,
to calculate the length of CD we use tangent ratio i.e,
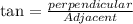
then;
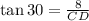 or
or
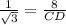
Simplify:
 cm.
cm.
Also, find the length of AC, we use sine ratio i.e,
 .
.
Then,
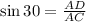 or
or

On simplify:
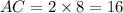 cm.
cm.
Now, in triangle ABC;
 ,
,
 then
then
 [Sum of the measure of the angles in the triangle is 180 degree]
[Sum of the measure of the angles in the triangle is 180 degree]
To calculate the length of BC;
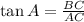 [∴
[∴
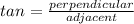 ]
]
therefore,
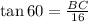
or
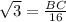
Simplify:
 cm.
cm.
Using Pythagoras theorem in triangle ACB;
Let BD be x cm
AB = 8+x cm , AC = 16 cm and
 cm
cm
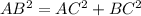
 or
or
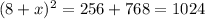 or
or

Simplify:
x=24 cm
Therefore, the length of AB = 8+x= 8+24=32 cm
Perimeter(P) of triangle ABC is equal to the sum of the sides of the triangle.
⇒ P= AB+BC+AC =
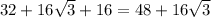 cm
cm