Question

Help me solve this math matrix equation please!!!

Answer 1

`\bf AB\implies \begin{bmatrix} 4&-2&3\\2&0&5 \end{bmatrix}\cdot \begin{bmatrix} -1&-4&3\\3&5&-3\\0&2&-2 \end{bmatrix}`

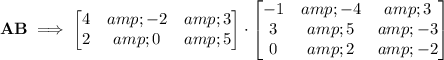
so, the way a matrix multiplication works is

we multiply the LEFT-Matrix ROW by the RIGHT-Matrix COLUMN, while adding each value.

namely, the row of (4, -2, 3) times (-1, 3, 0) and the sum of each will give us the first value for the product matrix, and the multiplication goes like this -> (4)(-1)+(-2)(3)+(3)(0), that gives us a sum of -4-6+0 = -10, and that is the value that goes on the upper-left-corner of the product matrix.

so let's do the whole thing.

`\bf AB\implies \begin{bmatrix} 4&-2&3\\2&0&5 \end{bmatrix}\cdot \begin{bmatrix} -1&-4&3\\3&5&-3\\0&2&-2 \end{bmatrix} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{lrlll} (4)(-1)+(-2)(3)+(3)(0)&=-10\\\\ (4)(-4)+(-2)(5)+(3)(2)&=-20\\\\ (4)(3)+(-2)(-3)+(3)(-2)&=12 \end{array}\impliedby \textit{the first row of the product} \\\\[-0.35em] \rule{34em}{0.25pt}`

`\bf \begin{array}{lrll} (2)(-1)+(0)(3)+(5)(0)&=-2\\\\ (2)(-4)+(0)(5)+(5)(2)&=2\\\\ (2)(3)+(0)(-3)+(5)(-2)&=-4 \end{array}\impliedby \textit{the second row of the product} \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ ~\hfill \begin{bmatrix} -10&-20&12\\-2&2&-4 \end{bmatrix}~\hfill`