Question

A straight rod has one end at the origin and the other end at the point (l,0) and a linear density given by λ=ax2, where a is a known constant and x is the x coordinate. since this wire is not uniform, you will have to use integrtation to solve this part. use m=∫l0dm to find the total mass m. find xcm for this rod. express your answer in terms of one or both of a and l.

Answer 1

It is given that a straight rod has one end at the origin (that is (0,0)) and the other end at the point (L,0) and a linear density given by
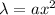`\lambda=ax^2`, where a is a known constant and x is the x coordinate.

Therefore, the infinitesimal mass is given as:

`dm=\lambda * dx=\lambda dx`

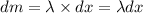
Therefore, the total mass will be the integration of the above equation as:

`\int\,dm= \int\limits^L_0 {ax^2} \, dx`

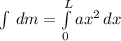
Therefore,
`m=a\int\limits^L_0 {x^2} \, dx=a[(x^3)/(3)]_(0)^(L)=(a)/(3)[L^3-0]= (aL^3)/(3)`

Now, we can find the center of mass,
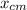`x_(cm)` of the rod as:

`x_(cm)=(1)/(m) \int xdm`

`x_(cm)=(1)/(m)\int_(0)^(L)x* \lambda dx =\int_(0)^(L)x* ax^2 dx=\int_(0)^(L)ax^3 dx`

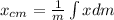
Now, we have

x_{cm}=\frac{1}{\frac{aL^3}{3}}\int_{0}^{L}ax^3dx=\frac{3}{aL^3}\times [\frac{ax^4}{4}]_{0}^{L}

Therefore, the center of mass,
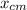`x_(cm)` is at:

`(3)/(aL^3)* [(ax^4)/(4)]_(0)^(L)=(3)/(aL^3)* (aL^4)/(4)=(3)/(4)L`