Question

Identify whether each value of x is a discontinuity of the function by typing asymptote, hole, or neither. 5x/ x3 + 5x2 + 6x

Answer 1

asymptote

asymptote

hole

neither

neither

neither

Answer 2

Function is discontinuous at

x=0 (Hole)

x=-3 (Vertical asymptote)

x=-2 (Vertical asymptote)

Explanation:

Given:
`f(x)=(5x)/(x^3+5x^2+6x)`

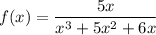
We need to identity the discontinuity of the function. As we know function is discontinuous where it is not defined.

So, The function is discontinuous at hole, asymptote and break point.

`f(x)=(5x)/(x^3+5x^2+6x)`

`f(x)=(5x)/(x(x^2+5x+6))`

`f(x)=(5x)/(x(x+3)(x+2))`

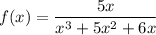
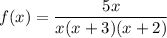
For hole, we will cancel like factor from numerator and denominator.

At x=0 we get hole.

For vertical asymptote, we set denominator to 0

x+3=0 and x+2=0

Vertical asymptote:

x=-3 and x=-2

Function is discontinuous at

x=0 (Hole)

x=-3 (Vertical asymptote)

x=-2 (Vertical asymptote)