Answer:
Option B.
Explanation:
Length of the fence = 100 feet.
Perimeter of the rectangular garden = 100 feet
2( length + width) = 100
Length + width = 50
Area of the garden is given by A = 50x - x²
If we draw the curve with area on y-axis and length on x axis, as shown in the picture attached,
Peak or vertex of the curve = [
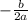 , A(-
, A(-
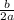 )]
)]
From the equation A = 50x - x²
a = (-1)
b = 50
So (
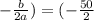 )
)
Therefore, for maximum area of the curve width = 25 feet
For x = 25,
Area of the garden = 50(25) - (25)²
A = 1250 - 625
A = 625 feet
Now area = length × width = 625
Length × 25 = 625
Length =
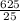
Length = 25 feet
Therefore, dimensions of the rectangular field are 25 feet by 25 feet.
Option B. will be the answer.