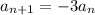Question

What is the recursive formula for this geometric sequence

4,-12,36,-108...

Answer 1

`a_(n+1)` = - 3
`a_(n)` with
`a_(1)` = 4

To find the next term in the sequence multiply the previous term by - 3

the common ratio r =
`(-108)/(36)` =
`(36)/(-12)` = - 3

`a_(n+1)` =
`a_(n)` × r ← recursive formula

Answer 2

Answer:
`a_(n+1)=-3a_(n)`

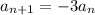
Explanation:

The recursive formula for geometric sequence is given by :-

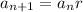`a_(n+1)=a_(n)r` -----(1) , where r = common ratio and n=natural number .

nth term of geometric sequence =
`ar^(n-1)`

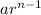
The given geometric sequence : 4,-12,36,-108...

First term =
`a_1=a=4`

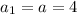
Second term =
`a_2=ar=-12`

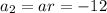
Also,
`r=(ar)/(a)=(-12)/(4)=-3`

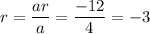
∴ r = -3

Put the value of r in (1) , we get the recursive formula for given geometric sequence as

`a_(n+1)=a_(n)(-3)`

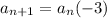
i.e.
`a_(n+1)=-3a_(n)`