Question

Graph the ellipse with equation x squared divided by 4 plus y squared divided by 49 = 1

Answer 1

`(x^2)/(4) +(y^2)/(49) =1`

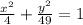
General equation is

`((x-h)^2)/(b^2) +((y-k)^2)/(a^2) =1`

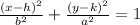
Where (h,k) is the center

From the given equation h=0 and k=0

So center is (0,0)

compare the given equation with general equation

b^2 = 4 so b= 2

a^2 = 49 so a = 7

`c=√(a^2 -b^2)`

`c=√(49 -4)=3√(5)`

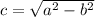
Vertices are (h, k+a) and (h, k-a)

We know h=0 , k=0 and a= 7

Vertices are (0,-7) and (0,7)

Foci are (h, k+c) and (h,k-c)

We know h=0 , k=0 and c=
`3√(5)`

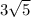
Foci are (0,-
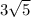`3√(5)`) and (0,
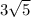`3√(5)`)

Answer 2

Answer with Step-by-step explanation:

We have to graph the ellipse:

`(x^2)/(4)+(y^2)/(49)=1`

when x=0 ,
`(y^2)/(49)=1`

i.e. y²=49

i.e. y= ±7

ellipse passes through (0,7) and (0,-7)

when y=0,
`(x^2)/(4)=1`

i.e. x² = 4

i.e. x= ± 2

i.e. ellipse passes through (2,0) and (-2,0)

The ellipse is shown as below: