Question

What value of k makes the equation true? (5a^2 b^3)(6a^k b)=30a^6 b^4

Answer 1

k = 4

Explanation:

`(5a^2 b^3) (6a^k b) = 30a^6 b^4`

We will solve the right side of the equation to find the value of k which makes this equation true.

Multiplying the terms on the left side of the equation to get:

`(5a^2 b^3)(6a^k b)`

=
`30a^(2 + k) b^7`

Now we can write it as

`30a^(2 + k) b^7 = 30a^6 b^4`

Now the power of a on the left side (2 + k) should equal the power of a on the right side (6) of the equation to make it true.

2 + k = 6

k = 6 - 2 = 4

Therefore, k = 4 makes the equation true.

Answer 2

we are given

`(5a^2 b^3)(6a^k b)=30a^6 b^4`

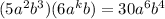
Firstly, we will simplify left side

and then we can solve for k

Left side is

`(5a^2 b^3)(6a^k b)`

we can arrange like terms

`(5a^2 6a^k)(b^3 b)`

`(5* 6 a^2a^k)(b^3 b)`

`(30 a^2a^k)(b^3 b^1)`

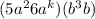
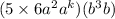
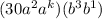
now, we can use property of exponent

`a^m * a^n=a^(m+n)`

`(30 a^(2+k))(b^(3+1))`

`30a^(2+k)b^(4)`

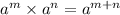
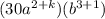
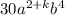
now, we can equate it with right side

and we get

`30a^(2+k)b^(4)=30a^6 b^4`

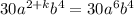
We can see that both sides have 30 , a and b

and they are equal

so, exponent of a must also be equal

`2+k=6`

now, we can solve for k

`2+k-2=6-2`

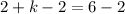
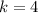`k=4`................Answer