Question

match each binomial expression with the set of coefficient of the term obtain by expanding the expression

Answer 1

By expanding the term
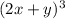`(2x+y)^3`, we get

`8x^3 + 12x^2y+6xy^2+y^3`.

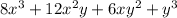Therefore, the coefficients for
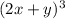`(2x+y)^3` are 8, 12, 6, 1.

By expanding the term
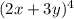`(2x+3y)^4`, we get

`16x^4+96x^3y+216x^2y^2+216xy^3+81y^4`.

Therefore, the coefficients for
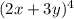`(2x+3y)^4` are 16, 96, 216, 216, 81.

By expanding the term
`(3x+2y)^3`, we get

`27x^3+54x^2y+36xy^2+8y^3`.

Therefore, the coefficients for
`(3x+2y)^3` are 27, 54, 36, 8.

By expanding the term
`(x+y)^4`, we get

`x^4+4x^3y+6x^2y^2+4xy^3+y^4`.

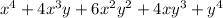Therefore, the coefficients for
`(x+y)^4` are 1, 4, 6, 4, 1.

Answer 2

`(2x+y)^3` =
`8x^3+12x^2y+6xy^2+y^3`

The coefficients are 8 , 12, 6, 1

`(2x+3y)^4`=
`16x^4+96x^3y+216x^2y^2+216xy^3+81y^4`

The coefficients are 16, 96, 216, 216, 81

`(3x+2y)^3`=
`27x^3+54x^2y+36xy^2+8y^3`

The coefficients are 27, 54,36 , 8

`(x+y)^4` = x^4+4x^3y+6x^2y^2+4xy^3+y^4

The coefficients are 1, 4, 6, 4, 1