Question

Which values are possible rational roots of 9x^3+14x^2-x+18=0 according to the rational root theorem? Select each correct answer. ±3 ±1/18 ±1/3 ±1/2

Answer 1

The possible rational roots are
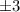`\pm3` and
`\pm(1)/(3)`

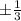
Step-by-step explanation

According to the rational roots theorem, the possible rational roots of

`9x^3+14x^2-x+18=0`

is given by all the possible factors of
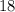`18` which are

`\pm1,\pm2,\pm3,\pm6,\pm9,\pm18`

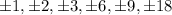
expressed over all the possible factors of the coefficient of the highest degree of the polynomial which is
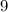`9` which are

`\pm1,\pm3,\pm9`

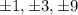
in their simplest form.

One of this possible ratios are
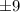`\pm9` from the factors of 18, over
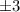`\pm3` from the factors of 9.

This will give us

`(\pm9)/(\pm3) =\pm3`.

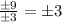Another possible rational root is

`\pm (1)/(3)`.

Hence the correct options are

A and C.

Secrete: Check if the denominator is a factor of 9 and the numerator is also a factor of 18, then these are the correct answers.