Solve sin(3x)=1/4 for all X, X in degrees

Question

asked Dec 11, 2019 60.8k views

1 Answer

Atheane · Answer 1 · 2019-12-16T06:01:36+0000

ANSWER

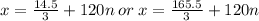$x=(14.5\degree)/(3)+120\degree n\:or\:x=(165.5\degree)/(3) +120\degree n$ , for
$n\ge 0$ , where
is an integer.

Step-by-step explanation

We want to solve the trigonometric equation;

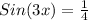
Sin(3x)=(1)/(4)

Since sine ratio is positive, it means the argument,
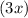(3x) is either the first quadrant or second quadrant.

This implies that;

(3x)=arcsin((1)/(4))

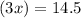$(3x)=14.5\degree$ in the first quadrant.

Or

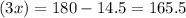$(3x)=180\degree-14.5\degree=165.5\degree$ in the second quadrant.

Since the sine function has a period of
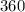$360\degree$ , The general solution is given by

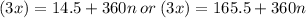$(3x)=14.5\degree+360\degree n\:or\:(3x)=165.5\degree +360\degree n$ ,for
$n\ge 0$ , where
is an integer.

Dividing through by 3, we obtain the final solution to be;

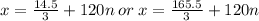$x=(14.5\degree)/(3)+120\degree n\:or\:x=(165.5\degree)/(3) +120\degree n$ , for
$n\ge 0$ , where
is an integer.