Answer:
The coordinate of point P(x,y) is,

Explanation:
Let the coordinate of the point P be (x,y) .
A point P divides a segment GH internally in the ratio m:n, to find the coordinate of point P we use the section formula :
The coordinate of point
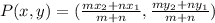
Then, to find the co-ordinates of the point P dividing the line segment GH joining two given points in a given ratio i.e m:n= 1:3.
Then,

 .
.
For y:
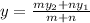
 .
.
Therefore, the coordinate of point P(x,y) is,
