Question

Classify each function as even, odd, or neither even nor odd.

Drag the choices into the boxes to correctly complete the table.



(SEE PICTURE)

Answer 1

Answer: f(x) is an even function, g(x) is neither odd nor even and h(x) is an odd function.

Explanation:

Since we have given that

`f(x)=x^6-x^4`

We will check it for even or odd:

Consider ,

`f(-x)=(-x)^6-(-x)^4=x^6-x^4=f(x)`

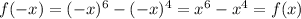
So, it is even function.

`g(x)=x^5-x^4\\\\g(-x)=(-x)^5-(-x)^4=-x^5-x^4\\eq g(x)`

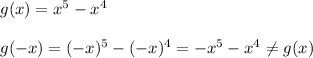
So, g(x) is neither even nor odd.

`h(x)=x^5-x^3\\\\h(-x)=(-x)^5-(-x)^3=-x^5+x^3=-(x^5-x^3)=-h(x)`

so, it is odd function.

Hence, f(x) is an even function, g(x) is neither odd nor even and h(x) is an odd function.

Answer 2

The function

f(x) is even

g(x) is neither even nor odd

h(x) is odd

Steps:

for an even function it holds that f(-x) = f(x):

f(-x) = (-1)^6 x^6 - (-1)^4 x^ 4 = x^6 - x^4 = f(x) => f is even

for an odd h(x) it holds that h(-x) = -h(x):

`h(-x) = (-1)^5x^5-(-1)^3x^3 = -(x^5-x^3) = -h(x) \implies h(x)\,\, \mbox{even}`

It is easy to show that g(x) does not match any of the two possibilities above.